|
|
针对于恒流量浇注这一课题,国内外学者均有研究,但其中大部分方法应用在真空感应浇铸系统中尚有不足之处。我所结合多年设计生产及使用经验,研究出一种恒流量的浇注算法,实现了非标炉型控制方法的快速开发,在降低成本的同时提高了工作效率。 ( f3 S z5 {" O' `% r! |" b
1、概述 " ]6 j. M* r6 u! C f" u
* ?) S M' f& p: I4 Y 恒流量浇注对于铸造、甩带、制粉等相关行业有着重要的实用意义。国内外对于低熔点的有色金属的恒流量浇注研究较多,已经有了很多专利及成功的经验。一般包括重力恒流量装置;通过加热管道,用泵或虹吸管实现定量输送;利用不接触式测距仪来实测液面高度进行反馈控制等方法。 % m6 k2 r( k3 r9 D" V' I& T! e
! f' g1 M u' y C* a4 J$ J 但以上这些相关技术在应用上不适用于真空感应炉。在真空熔炼炉中,通过角度控制达到恒流量浇注的方法是比较可行的。国内外很多人已经对此有了一定的研究,如李详红等人对恒流量控制的研究。国内的研究主要针对大气浇注设备,对于真空炉的应用有局限性。而且在数学建模方面,国内学者无一例外的采用传统符号计算理论模型,对坩埚进行简化处理,这方面上是有一定欠妥的。我所根据多年设计研究经验探索出一套利用三维模拟快速建立恒流量控制的方法,适用于非标炉型控制系统的快速开发。极大的提高了工作效率,并为客户提供了恒流量浇注的解决方案。
( j* u' [) Z6 u7 S3 p2、建立数学模型 & {- W) S( ~4 d
3 e! X+ K* A# h& _9 n. N( B8 S1 r
2.1、与传统方法的对比
3 H6 B& ? @4 T- D- e- K7 X$ F; k$ N' w2 u* b. U
采用三维模拟采集数据建立的数学模型更为精准。而传统方法则是利用坩埚倾转与流量浇出的数学关系建立一个分段函数,通常为了推导的方便国内多数学者都将坩埚模型的锥度进行简化处理(处理成圆桶,无锥度)。再根据浇注的三个阶段推出一个分段函数,即从0 度到临界出液为一段;出液到截面恰为三角形为一段;三角形到浇完为一段。图1 展示了这三段过程。
0 f: i" b" |& y0 V* d: {2 V
' t2 R7 b! x" e2 d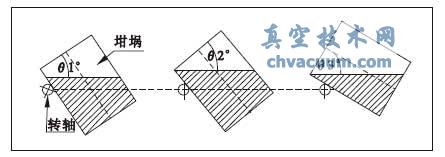
. D# V$ f% |1 N1 }1 `3 [ E$ J2 }& X
图1 简化的坩埚浇注三个阶段 7 p; _9 q, r" d4 ?! W F
, B( h% d% s; s: V& B. X- F( x
而使用三维模拟的方法则不同,不必对坩埚模型进行简化,而是直接利用强大的三维软件直接对浇注过程进行模拟并采集数据,再进行数学建模。
6 J! z$ M4 F, N7 ]. a
: s9 b( x1 \' U+ \2 Z) v 2.2、翻转三维模拟与数据采集 1 {! I+ x- U# L4 l' `) T' o
- ~. W- G! g# Y* W 利用三维CAD软件建立坩埚与钢液三维模型并装配,坩埚保有实际中的锥度。再利类似有限元理论中的“非线性”思想,设计不同角度的算例(用离散法采集坩埚在不同倾角时,坩埚内钢液的体积。对于从0 度位到钢液临界位,由于此段无液体流出,所以不在采集范围内,只要找到该临界点即可,此过程不再赘述。本文以VIPF 喷粉炉熔炼系统为例,转轴位置与VIF 感应熔炼炉略有不同。 : e' i" V8 F4 ~4 r; r
2 ~( E- L. ~, k4 V" U/ T( r
由于是针对“三段”中的后“两段”进行模拟,所以有两组数据,下图展示了由第二组数据生产的离散点图。整个模拟过程的步长为0.25 度,即每转0.25 度记录一次体积。借助三维软件及强大的计算资源得到了近200 个样本的分析数据。 , K5 Z/ j4 m% C. J5 C8 g( @
" W' P1 U; X% v5 E& A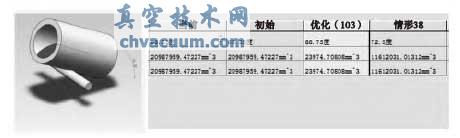 2 Y# }4 b5 w6 N( P 2 Y# }4 b5 w6 N( P
, g" j1 L& X7 g% L7 H
图2 三维模拟 & k+ S; w9 t, p) o
% I9 \2 `$ M R
2.3、利用数值分析法建立volume-angle 数学模型 ; `; x& U& Y( S0 }6 r3 G
; p3 Y# w% Q0 U" V 将得到的数据进行处理后导入Matlab 中进行分析建模。利用Matlab ToolBox 中的Curve Fitting Tool 将导入的数据进行曲线拟合,尝试得到适合的函数式。通过绘制离散点图我们发现VIPF 型真空喷粉炉的两段数据连续性很好,完全可以将两组数据拼接进行建模(其它炉型,可分段处理)。我们运用了多种方式进行曲线拟合,从实际情况及数学原理上看多项式效果较好。图3、图4展示了分别用多项式(二次、三次、四次)和幂函数拟合的效果及拟合程度。 * x6 d5 _% R, ~ y8 q/ k8 @
: B( m+ E3 v* J- e4 U
从Matlab 生成的Goodness of fit (拟合程度)上看,三次与四次多项式的效果较好四项指标:SSE、R-square 、Adjusted R-square、RMSE (指标的数学意义参考文献[4-5])均很理想。鉴于四次拟合的P1 项很小(6.239e-006)且拟合结果与三次很相近。同时从三次多项式拟合曲线的残差图(见图5)上分析,曲线的绝大部分拟合情况良好(95%以上),曲线后期拟合情况不好主要是坩埚有较小的弧度,这个小角度在浇注末期熔液所剩无几时所产生的影响相对变大所致,因此在工程应用中可以不计。 ' }' Q& F5 ~7 n$ |) {
4、实际应用与误差分析
4 k \: L& c( v) e/ ?: ^+ ^8 X( g2 w) a E% K/ U
此套算法开发后在实际工程中得到了应用,收到了较为理想的效果。以往对于VIPF 系列炉,常常出现由于浇注速度不稳定而导致中间包堵死或断流等现象。应用以此算法为核心的控制方法后,降低了此类事件发生的可能性,收到了令人满意的效果。该算法在速凝甩带炉中也得到了很好的应用。
- [/ A/ o: w8 D2 t
( {- x9 v, I$ P 此套算法以数学模型为核心,接合闭环控制方法。对于实际工程应用来说较为理想。但从学术角度来讲,还存在着一定的误差。主要来自三方面:
- G+ h- ?, s; Z0 P& m5 C- ]7 o9 i, D9 X- H
(1)数学模型原理性误差:是数值运算不可避免的,可通过提高精度来减少,但过高的精度有碍于建立简洁的数学模型。
7 L8 Y+ j' A% E. B) g- ^5 {2 ]4 d- j& I8 B- P% k+ Q
(2)物力模型原理性误差:物理模型简化所致,若进一步提高精度必须考虑钢液粘性以及钢水溅射机理等方面因素。日本学者K. Shinohara和H. Morimoto 在以上几方面有大量研究。
, l6 u3 b/ ?/ A9 Y7 P! \+ p2 B9 k& C( @. f
(3)控制系统误差:控制算法、传感器、驱动系统都会产生一定的误差。
' F# t E5 u: N5 Z( q1 I7 a5、总结
5 W; y/ \0 W. Q1 h4 s3 ?3 s; S# Q. i y1 ^' f9 {( } E
综上所述,本文所探究恒流量浇注算法是一种面向工程应用、权衡各方面成本及精度的一种控制方法。特别适用于大中型真空感应熔炼浇铸设备。该方法有助于提高设备的整体自动化程度,同时提高了产品的质量及生产效率。 |
|