|
|
KTX 为中国科学技术大学在建的反场箍缩实验装置,在同类装置之间,其参数介于美国MST 和意大利的RFX 之间。KTX 真空室壁厚仅为6 mm,属于非标准环形薄壳结构,其结构的稳定性分析是确定结构设计是否合理的关键因素。本文利用有限元的方法,对KTX 真空室结构进行了线性和非线性屈曲分析。得到了两种情形下应力和变形加载曲线。通过对计算结果的对比和分析,验证了目前真空室结构的稳定性符合要求,并具有一定的安全裕度。
% C/ T/ B5 c2 h" h& ~* B, T9 I+ j! o+ v/ k5 L' |
KTX 装置是一个反场箍缩实验装置,是有别于托卡马克、仿星器位形之外的环形磁约束等离子体聚变装置。它具有工程简单、比压高以及欧姆加热直接可达点火条件等优点,是先进磁约束聚变位形探索的重要方向。KTX 装置主机主要由24 个纵向场线圈,20 个极向场线圈,16 个平衡场线圈,真空室,导体壳,鞍型线圈,真空抽气系统及其各类支撑和支撑平台等部分组成。 ( _- c0 T" d2 }& Q
4 v7 G) f+ @( i* K8 \4 o+ n
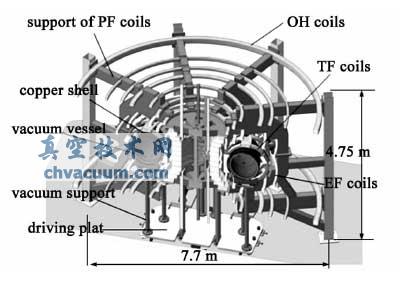
所有磁体线圈实验时采用被动冷却,真空室采用双C 结构连接密封。其主要设计参数为:大半径1.4 m,小半径0.4 m,最大等离子体电流1 MA,电子密度2 × 1019 m-3,电子温度约600 eV,放电时间30~100 ms。整个KTX 装置高约为4.75 m,直径为7.7 m。装置尺寸与目前美国的MST 装置相当,但电流将超过MST,仅次于意大利的RFX 装置。图1给出的是KTX 装置总体设计的剖视图。
8 {7 v6 M7 f! q4 B" d; q4 d
2 s) }# u& r5 U7 A g+ z+ \, ], n0 G KTX 真空室内部真空度可达1.3 × 10-6 Pa,属于高真空负压容器,同时其壳体厚度仅为6 mm。诸如此类具有很大半径厚度比的环形真空室结构,其抽完真空之后可能会因结构失稳而造成破坏性的后果。鉴于此,真空技术网(http://www.chvacuum.com/)认为KTX 真空室结构稳定性分析与评估是决定设计方案是否合理的关键性因素。
; w0 P, f4 O, }- E4 a+ L
9 q% w& W/ w! ^6 q7 t d 众所周知,屈曲计算中的临界压力可以根据经典的欧拉公式得到理想情况下的数值解,但是对于几何特征不规则的结构,欧拉公式能起到的作用却十分有限。相比较而言,利用有限元的方法进行稳定性校核,其适用范围则更广,可以处理更加复杂的结构。并且,通过对线性和非线性屈曲计算结果的对比分析,计算的可靠性较高,具有更好的实用性,对同类的工程问题有很好的参考价值。
G! U3 ~% u: I) N; x5 i3 W2 z6 H$ s- O6 `; e$ O- O7 B
 . D3 J- I; u2 g' j& g . D3 J- I; u2 g' j& g
, o6 r$ Q! W/ p1 p a& H; s' n
图1 KTX 装置总体设计剖视图 5 N( j0 M0 `2 l
1、KTX 真空室结构及有限元建模 % D; e# a8 C. B2 a2 E1 P
9 a" ]2 d& f7 H- I" T! v5 c( z KTX 真空室结构主要包括真空室本体(SS316L不锈钢,6mm) ,外层的导体壳( 无氧铜,1.5 mm) 以及两者之间的绝缘层(5 mm) 。真空室本体主要作用是维持10-6 Pa 的真空度,为内部部件提供安装空间及承受等离子体破裂和垂直位移条件下的电磁力。为了便于维护,真空室采取双C 结构设计,可以保证其在径向各自向后移动150 mm 的距离,双C 真空室之间由真空密封法兰连接。
+ R% u' k& Y/ _( f: l, @% R
, l. j' L9 e& q) `+ r% v 根据物理设计要求,在真空室外表面设计包裹有一层导体壳,厚度为1.5 mm,其主要作用有:在等离子体击穿前,增大等离子体环电压用于击穿等离子体;在等离子体击穿后,导体壳上感应电流产生磁场稳定等离子体。同时,为了满足装置实验期间的抽气、测试和诊断等不同功能需求,真空室上开有很多大小不等,分布不均的窗口。 ( @3 K% f' S* y8 @" A$ S; z& w
( r2 S5 w5 u( ~# F, Q6 ], o% u4 h
屈曲计算中,主要目的是为了得到薄壳形式的真空室不发生屈曲变形的临界压力。建模时,主要包括真空室、铜壳及之间的绝缘层。考虑到真空室开孔对屈曲临界压力的影响,模型中的开孔均按原尺寸建立。真空室支撑没有建出,用在真空室受支撑表面添加全约束的方式替代。图2 所示为KTX 真空室结构和简化后的有限元模型。
$ ]; J. N1 z2 p0 @- D
. X9 r: l- N- ?* |" s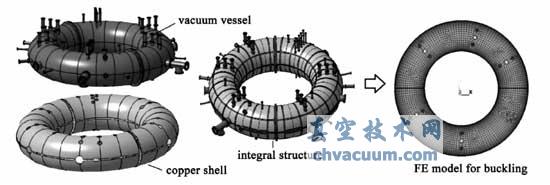 : z4 r# @* S* I2 ]0 X- g : z4 r# @* S* I2 ]0 X- g
7 s% \% v% Z2 F9 b% ]3 z& {
图2 KTX 真空室结构及有限元模型 i- Q5 E. E! [! p
2、真空室线性屈曲分析 $ t' J3 V: L( V+ I
% _9 M2 `; q( t2 P 利用有限元方法对KTX真空室结构进行线性屈曲分析,其原理相当于理论计算中的求解线性稳定性方程的特征解。线性屈曲计算的结果是基于几何和材料完全理想的条件下得到,是非保守值,主要用于预测理想线弹性结构的理论屈曲强度,估算结构屈曲临界压力的大致范围,同时也能为后面的非线性屈曲计算提供参考量。线性屈曲分析中的模型建立和网格划分与静力有限元计算无异,其主要区别在于求解类型及模态扩展的设置,除了真空室的支撑约束之外,在薄壳型真空室表面施加单位压力载荷。 : O0 z5 N. v! d8 d0 [" Q# e
8 j' @# W2 E: o4 F( J3 R$ @ 结果中得到的不同屈曲模态下的频率即为真空室结构线性稳定性方程的特征值解,也即线性临界压力pcr。如图3 所示,一共提取了真空室屈曲变形的四种模态,相应屈曲模态下的临界压力递增,分别为6.17,6.49,6.61 和6.71 MPa。其中,前两种模态的变形阶数n = 3,后两种n = 4。 * J' J0 y3 c# h0 s4 t
: p! P# i+ v! E+ N& V& g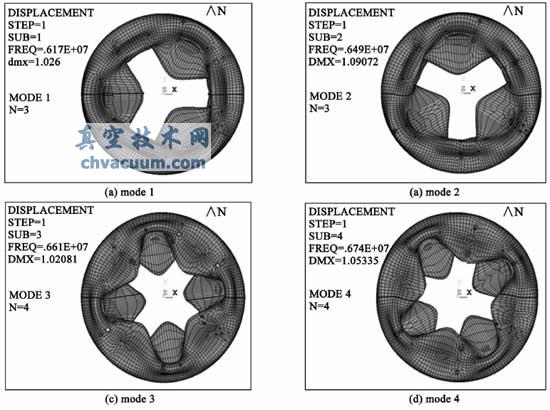
% U9 ^" G1 T4 ~* b6 F$ f9 M( s# F+ M1 g, e9 L
图3 KTX 真空室线性屈曲计算结果
1 v k$ `8 H% W: ]3、非线性屈曲分析 # c& E5 L! U% N; B) b& ?9 m4 a4 [7 y
! u% Y( F8 O' U. [' q* \" F 由于基于稳定性特征方程的线性屈曲分析没有考虑任何非线性因素和几何初始缺陷,因此它得到的通常是非保守解,一般不在工程实际中应用。为了得到KTX 真空室结构失稳临界压力的保守解,需要对结构及材料的非线性因素和几何缺陷进行拟合。具体拟合方法为:
& ?5 p! k, f) W9 i5 k% Q9 R( k, D' m C5 Z
将线性计算的特征值解作为载荷参量施加( 因为非线性失稳压力小于线性解,加载因子从零开始到最终收敛时的值应小于1) ;考虑KTX真空室结构几何非线性因素,将几何初始缺陷取为线性分析中变形结果的1%;考虑材料非线性因素,由于非线性屈曲伴随着结构的大变形,且可能已经超出材料弹性变形的范围,因此需要对材料模型进行修正。将材料的屈服应力设置为195 MPa。
: g" r* D& R" Y' R. y: X X7 t
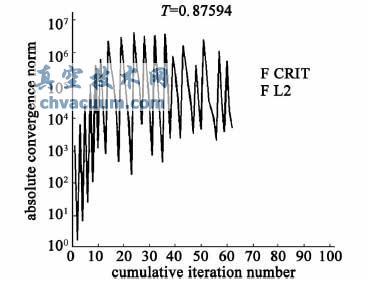
) l( c; P* w& L9 N7 C* q0 C4 W! s 非线性屈曲分析中,以线性计算得到的第一模态的临界压力6.17 MPa 为基准加载,即相当于61个大气压外力作用。得到的整体收敛因子为0.87594,如图4 所示。 ! e8 l- R. C4 W V8 @8 Z
$ T$ g N& E; w# B6 w/ b2 s* m
 ' P, s( W2 G5 _# U- V; r' f) D ' P, s( W2 G5 _# U- V; r' f) D
# k& ~! Q/ C1 u图4 KTX 真空室非线性屈曲收敛曲线
0 {& [" |5 l5 k
: E9 _& Q5 O6 `6 j L- d. E5 f 为了进一步分析,提取真空室双C 接口处最大应力节点和真空室开孔处一应力集中节点的计算结果分别绘制加载曲线( 如图5) 和两个关键节点的应力_变形曲线( 如图6) 。 ' W' n" q* @+ `6 n
4 D2 X. @! U$ j5 e (1) 几何非线性:由图5 中两个特殊节点的变形加载曲线可以看出:当加载因子约为0.86 时,出现明显非线性趋势,可视为屈曲。
6 E1 i9 ^( C% F$ v6 L$ n3 i$ D. R2 j; S6 w
(2) 材料非线性:由图5 中两个特殊节点的应力加载曲线可以看出:加载因子为0.34 时,应力曲线出现明显非线性趋势,可视为应力值达到材料屈服极限,材料发生屈服。 6 ?% z4 v2 c. n6 M! B8 v
' `. e A9 l4 Q* s% \
(3) 进一步验证:由图6 中两个节点的应力变形曲线可以看出:当材料发生屈服时的临界变形值分别为3.6 和3.8 mm,再一次观察图5 的变形加载曲线,发生相应变形时的加载因子均约为0.34,符合材料非线性的加载规律。 ; |+ a4 l; N3 T9 ^
1 }: |1 c6 x" ~# r9 n2 H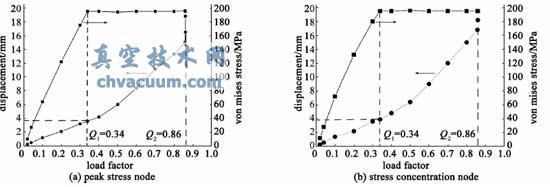
% Y; W% |* B: ]' w9 U7 l: |9 E' \) K; X/ b8 X4 b5 B0 O, q- D
图5 KTX 真空室非线性屈曲关键节点加载曲线
5 y- L- l8 W# I
5 }9 H- K% R' q1 x" O 综合考虑两种非线性因素可以得出:真空室在发生屈曲之前就已达到材料的屈服极限,即不会发生屈曲,KTX 真空室结构设计符合稳定性要求。结构校核只需满足材料的强度要求即可; 在屈曲计算中,应力达到屈服强度的加载因子为0.34,即材料不发生屈服的临界压力为pcr = 6.17 * 0.34 = 2.0978MPa,相当于21 个大气压的作用。在之前的极端工况( 等离子体破裂) 下的电磁力计算中,KTX 真空室承受的瞬态电磁力最大相当于约1.75 个大气压的作用,考虑本身外压1 个大气压,即真空室最大承受2.75 个大气压,安全因子为n = 21/2.75≈7.6。 2 X- E, D; X( ` U2 K. F
4 E: b ]) z, l$ A7 g" m; @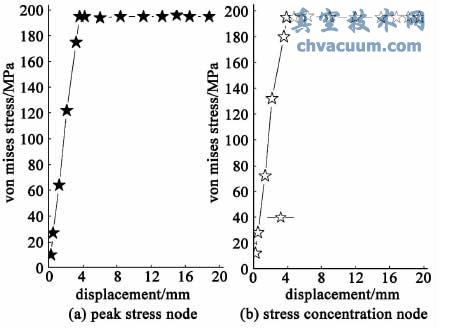
0 v3 u- g: u2 t# }" L
& k& t6 z: y9 Q4 h& @% x8 j+ |图6 KTX 真空室关键节点应力变形曲线 ! A) J r. z5 ]9 F2 z% ?
4、结束语 % H6 Q, |, N& F* s2 m* o9 L8 q
5 Z7 @2 Z+ A; `$ g, k
本文结合KTX 薄壳型真空室稳定性设计的实际工程问题,利用有限元的方法,进行了线性和双非线性屈曲计算及相应的结果分析。计算结果验证了KTX 真空室结构设计符合稳定性要求,且具有足够的安全裕度,为真空室进一步细化设计提供了参考和依据。目前,KTX 真空室的本体结构已经初步加工完成,等待进一步的开孔、焊接、表面处理等后续工序。同时,值得强调的是,本文阐述的有限元屈曲分析思路和方法对其他难以用经典欧拉公式直接求出临界压力的不规则结构的稳定性校核同样适用,对解决同类工程问题具有一定的参考意义。 |
|