对地球大气密度随高度分布规律的讨论

[db:作者]

　　以NASA大气模式MSISE-1990为依据,用实例验证的方式证明了关心大气成分的数密度时,玻耳兹曼能量分布律仅适用于几公里至几十公里高度以内的分子态气体。考虑重力加速度随高度变化时,用该分布律得到的无限高处大气数密度在数学形式上不为零,但从物理角度分析其值与零没有差别。忽略重力加速度随高度变化时,用该分布律得到的无限高处大气数密度在数学形式上似乎为零,但无限高处重力加速度应为零,因而不能解决无限高处大气数密度在数学形式上不为零的问题。计算大气分子总数时,积分上限只需数十公里。考虑重力加速度随高度变化时,用该分布律计算大气分子总数的积分发散,因此上限不应超过数百倍地球半径忽略重力加速度随高度变化时无此限制。达道安等人(宇航学报,2006,27(06) :1306-1313)对该分布律导出的大气密度随高度分布所作的修正,不仅在数学形式上解决了无限高处大气数密度不为零的问题和计算大气分子总数的积分发散的问题,而且在有实际意义的范围内与该分布律精密吻合。
+ q8 V$ S$ x6 x1 G& n1、由玻耳兹受能分布律导出的大气密度随高度分布
7 D5 h$ R) U9 G6 B$ J* f　　1687年牛顿发表了万有引力定律, 1859年麦克斯韦导出了平衡态下气体分子的速率分布定律,尔后,玻耳兹曼发展了麦克斯韦的分子运动学说,证明了在有势的力场中处于热平衡态的分子速度分布定律,即玻耳兹曼能量分布律。麦克斯韦-玻耳兹曼分布律是对相互作用可忽略的大量同类气体分子的集合,采用概率统计的方法导出的川。玻耳兹曼能量分布律的表达式为：
' E% s, J" R9 e2、由大气模式得到的大气密度随高度分布
5 `+ g+ V5 q8 k6 Q( d; E4 g2.1、大气层的温度分布
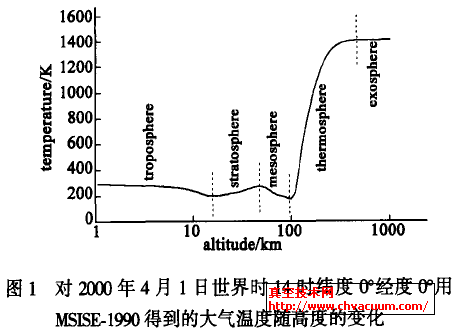
  K& C4 p2 x# b　　大气层可以被粗略地表征为环绕地球从海平面到大约1000Km高度的区域,其间电中性气体可以被检测。50Km以下该大气可以被假定为均匀混合的而且可以被当做一种理想气体。80Km以上该流体静力学平衡因扩散而逐渐崩溃且垂直输运变得重要。在上层大气中主要的气体种类是N2，O，O2，H，He。按温度的垂直分布可将大气层分为对流层,从海平面直到大约10Km,其间温度逐渐降低，同温层，从10Km直到大约45Km,其间温度逐渐上升，中间层,从45Km直到大约95Km，其间温度再次逐渐降低，热层，从95Km直到大约400Km，其间温度再次逐渐上升；而外逸层，大约在400Km以上,其间温度是常数。
　　图1给出了对2000年41日、世界时14时、纬度0o、经度0o用NASA大气模式MSISE-1990的执行软件得到的大气温度随高度的变化,图中太阳F10.7通量前一天和三个月平均和地磁AP指数一天是该执行软件利用已存储的1961年1月至2006年8月范围内太阳辐射强度和地磁活动指数的变化信息自动给出的。

! @2 D- J+ U. u2 p0 L9 P# @) w　　限于篇幅，文章第二章节的部分内容省略，详细文章请到论坛下载：对地球大气密度随高度分布规律的讨论。
6 R/ b8 P- o) A' ~' [5、结论
" n) H" g' b8 i. l2 l" T2 ^+ B4 B0 i& l- U　　(1)MSISE-1990模式以实测数据为根据,得到的大气密度随高度分布是真实可信的。用以计算大气分子总数时,积分上限只需数十公里便足够准确；
: K" S, W' K* v3 ]( g　　(2)关心大气成分的数密度时,玻耳兹曼能量分布律仅适用于几公里至几十公里高度以内的分子态气体包括无所谓原子态还是分子态的惰性气体,但不包括O,H,N等原子态气体；
　　(3)考虑重力加速度随高度变化时,用该分布律得到的无限高处大气数密度在数学形式上不为零,但从物理角度分析其值与零没有差别忽略重力加速度随高度变化时,用该分布律得到的无限高处大气数密度在数学形式上似乎为零,但无限高处重力加速度应为零,因而不能解决无限高处大气数密度在数学形式上不为零的问题；
　　(4)考虑重力加速度随高度变化时,用该分布律计算大气分子总数的积分发散,因此上限不应超过数百倍地球半径忽略重力加速度随高度变化时无此限制；
　　(5)达道安等对该分布律导出的大气密度随高度分布所作的修正不仅在数学形式上解决了无限高处大气数密度不为零的问题和计算大气分子总数的积分发散的问题,而且在有实际意义的范围内与该分布律精密吻合。
5 M: c) v- ^" ?  b　　对地球大气密度随高度分布规律的讨论